Four‐Connected Components in a Binary Matrix

Given a positive integer \( n \), we construct a \( 2^n \times n \) matrix in the following way: for every integer \( i \) in the range \( [0,2^n) \), write its lowest \( n \) binary digits from least significant to most significant into row \( i \) of the matrix. Both row and column indices are 0-indexed.

For example, when \( n = 3 \), the matrix looks like:

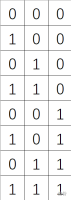
You are then given \( q \) queries. Each query consists of two integers \( x \) and \( y \), representing the coordinates of a cell in the matrix. For each query, determine the size (i.e. the number of cells) of the 4-connected component (neighbors connected in the four cardinal directions) that contains the cell \( (x,y) \). Two cells belong to the same component if they have the same value (either 0 or 1) and they are connected via adjacent moves (up, down, left, right). Output the answer modulo \( 998244353 \).

Note on the Matrix Construction: The entry in the cell at row \( i \) and column \( j \) is given by:

[ A(i,j)=\left(\frac{i}{2^j}\right)\bmod 2. ]

This guarantees that the binary representation is written from lower order bits (column 0) to higher order bits (column \( n-1 \)).

inputFormat

The first line contains two integers \( n \) and \( q \), where \( n \) is the parameter for the matrix and \( q \) is the number of queries.

Each of the next \( q \) lines contains two integers \( x \) and \( y \) (0-indexed), representing a query for the cell at row \( x \) and column \( y \).

outputFormat

For each query, output a single line containing one integer: the size of the 4-connected component that contains the cell \( (x, y) \), taken modulo \( 998244353 \).

sample

3 3
0 0
2 0
6 1

7
1
5