Generalized Segment Tree Updates

You are given two sequences a and b of length n and a generalized segment tree built on a with exactly 2n-1 nodes. In the generalized segment tree, each node p has an interval \([L_p,R_p]\) and an associated weight</em> \(M_p=\prod_{i=L_p}^{R_p} a_i\) in \(\LaTeX\) (i.e. the product of all elements in the interval). The tree satisfies the following properties:

• All nodes with indices \(p\in [n,2n-1]\) are leaves, and for each such node, \(L_p=R_p=p+1-n\).
• All nodes with indices \(p\in [1,n-1]\) are non-leaf nodes. For each non-leaf node \(p\), there exist two children \(X_p\) and \(Y_p\) (with \(p<X_p<Y_p\)) such that the interval of \(p\) is the union of the intervals of its two children. Formally, if the left and right children of node \(p\) are \(X_p\) and \(Y_p\) respectively then \(L_p=L_{X_p}\), \(R_p=R_{Y_p}\) and \(R_{X_p}=L_{Y_p}-1\).

For example, when \(n=4\) and \(a=[1,2,3,4]\), one possible generalized segment tree is as shown below:

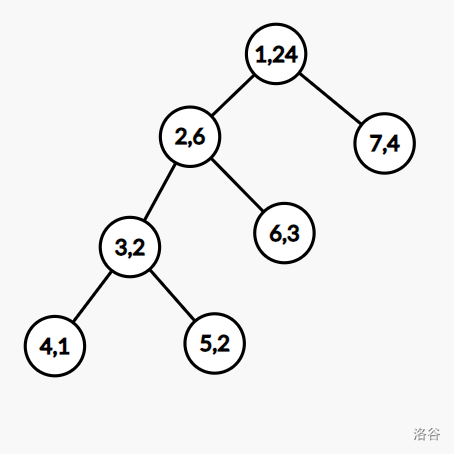
You will be given the sequences a and b along with the shape of the tree \(T\) (i.e. the indices of the left and right children for each non‐leaf node). Then you must perform exactly n operations where the i-th operation is to update \(a_i\) as follows:

[ a_i \gets a_i \times b_i ]

After each update, you are to rebuild the generalized segment tree using the updated sequence a (keeping the same tree shape) and compute the sum of the weight values of all nodes:

[ S = \sum_{p=1}^{2n-1} M_p \mod 998,244,353 ]

Output the value of \(S\) (modulo 998244353) after each operation.

inputFormat

The input is given in the following format:

 n
 a1 a2 ... an
 b1 b2 ... bn
 X1 Y1
 X2 Y2
 ...
 Xn-1 Yn-1

Here, the first line contains an integer n, the lengths of sequences a and b. The second and third lines list the sequences a and b respectively. The next n-1 lines describe the binary tree structure. For each non-leaf node p (\(1 \le p \le n-1\)), the corresponding line contains two integers \(X_p\) and \(Y_p\) representing the indices of its left and right children respectively. Note that the nodes with indices \([n,2n-1]\) are leaves.

outputFormat

Output n lines. The i-th line should contain a single integer representing the sum of all node weights \(\sum_{p=1}^{2n-1} M_p\) modulo 998244353 after the i-th update.

sample

4
1 2 3 4
2 2 2 2
2 7
3 6
4 5

75
141
264
460

</p>