Coloring Squares Game

There is an \(n \times n\) grid composed of small squares with side length \(1\). Two players, Walk Alone (who colors edges red) and Kelin (who colors edges blue), compete in a coloring game. They take turns selecting an uncolored edge of any square, with Walk Alone moving first.

The rules are as follows:

1. When it is Walk Alone's turn, he chooses an uncolored edge and colors it red. After his move, if this edge completes the boundary of one (or two) square(s), that square is automatically filled with red.
2. When it is Kelin's turn, he chooses an uncolored edge and colors it blue. After his move, if this edge completes the boundary of one (or two) square(s), that square is automatically filled with blue.
3. The game ends when all edges have been colored. The winner is the player whose color fills more squares; if both have the same number of squares, the game is a draw.

For example, in a \(2 \times 2\) grid, one possible sequence of moves is illustrated below:

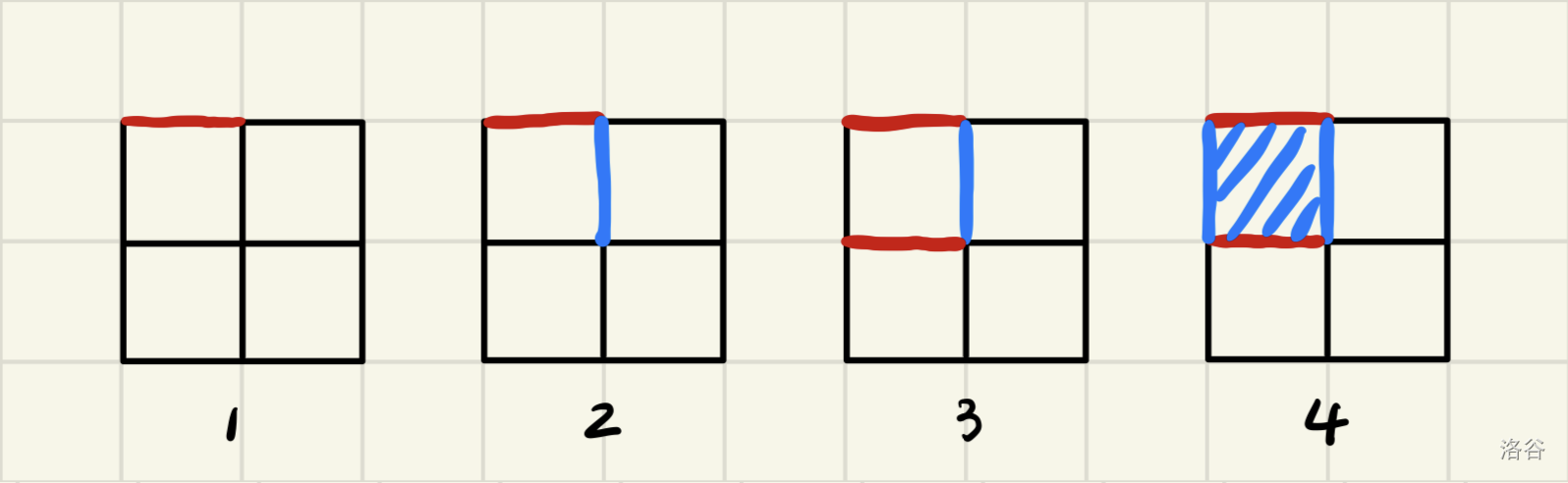
inputFormat

The input consists of a single integer \(n\) (\(1 \le n \le 10^9\)), representing the side length of the grid.

outputFormat

Output a single string: "Walk Alone" if Walk Alone wins, "Kelin" if Kelin wins, or "Draw" if the game ends in a tie, assuming both players use an optimal strategy.

sample

1

Kelin