Connected Lego Wall

You are given two kinds of LEGO blocks: a $1\times1\times1$ block and a $2\times1\times1$ block (width, height, length). There are infinitely many blocks of each type. All blocks of the same size are identical. Each block is used in its proper orientation. The four side faces of a block are made of the same material, and aside from the size, there is no difference between the two types of blocks.

We say two blocks are locked if and only if one block is placed directly on top of the other. Two blocks $b_0$ and $b_k$ are called connected if and only if there exists a sequence of blocks $b_0, b_1, \ldots, b_k$ such that for every adjacent pair $b_{i-1}$ and $b_i$, one block is placed directly on top of the other. A set of blocks is said to be connected if every pair of blocks in the set is connected.

You wish to build a LEGO wall of size $w\times h\times 1$. The wall must satisfy the following two conditions:

• No holes: The wall must completely cover a $w\times h$ rectangular area (each level is fully tiled).
• Connected: When considering the graph whose nodes are the blocks and there is an edge between two blocks if one is directly on top of the other, the entire set of blocks must form a single connected component.

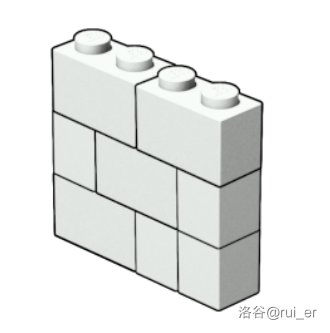
For example, the following $4\times 3\times 1$ LEGO wall is valid:

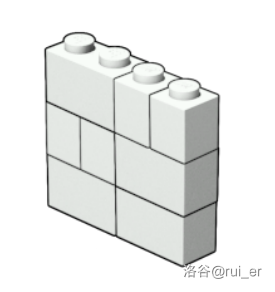
However, the following $4\times 3\times 1$ wall is not connected and is therefore not allowed:

You have an unlimited supply of $1\times1\times1$ and $2\times1\times1$ blocks. Note that a $2\times1\times1$ block can only be placed horizontally (covering two adjacent cells in the same row); vertical placement is not allowed. Two tilings that are mirror images (rotated $180^\circ$) of each other are considered different unless they are identical.

Calculate the number of ways to build a wall with no holes and that is connected. Since the answer may be very large, output it modulo $10^9+7$.

Explanation of the connectivity condition:
Consider the wall as being built row by row. In each row, the tiling covers the entire row with blocks (each block is either a monomino covering a single cell or a domino covering two adjacent cells). The only way for blocks to connect is when a block in row $i+1$ is placed directly on top of a block in row $i$ (i.e. the block in row $i+1$ overlaps with the block in row $i$ in at least one column). Note that blocks in the same row are not directly connected. The overall wall is valid only if the graph defined by vertical connections is connected.

inputFormat

The input consists of a single line containing two integers $w$ and $h$ ($1 \le w, h \le \text{small}$), which represent the width and height of the wall respectively.

outputFormat

Output a single integer: the number of ways to build a valid LEGO wall (with no holes and connected) modulo $10^9+7$.

sample

1 1

1