CSP-J 2202: The AK Challenge

After a brief disorientation, you realize that you are sitting in a computer room in the year 2202 – specifically, in the contest hall of CSP-J 2202.

Before you lies a challenge that consists of four different problems. A mysterious voice whispers: "Want to know what’s going on? Then demonstrate your past abilities and beat this CSP-J as easily as before!"

The four tasks are as follows:

1. Given a positive integer \(n\), compute \(\lfloor \sqrt{n} \rfloor\).
2. You are given a bipartite graph with \(n\) vertices on each side and \(m\) edges. Compute the number of perfect matchings modulo \(998244353\).
3. Conway's Game of Life is played on an infinite two-dimensional grid. Each cell is either empty or occupied by a cell. At every iteration, the following rules are applied (see the image for details):
   
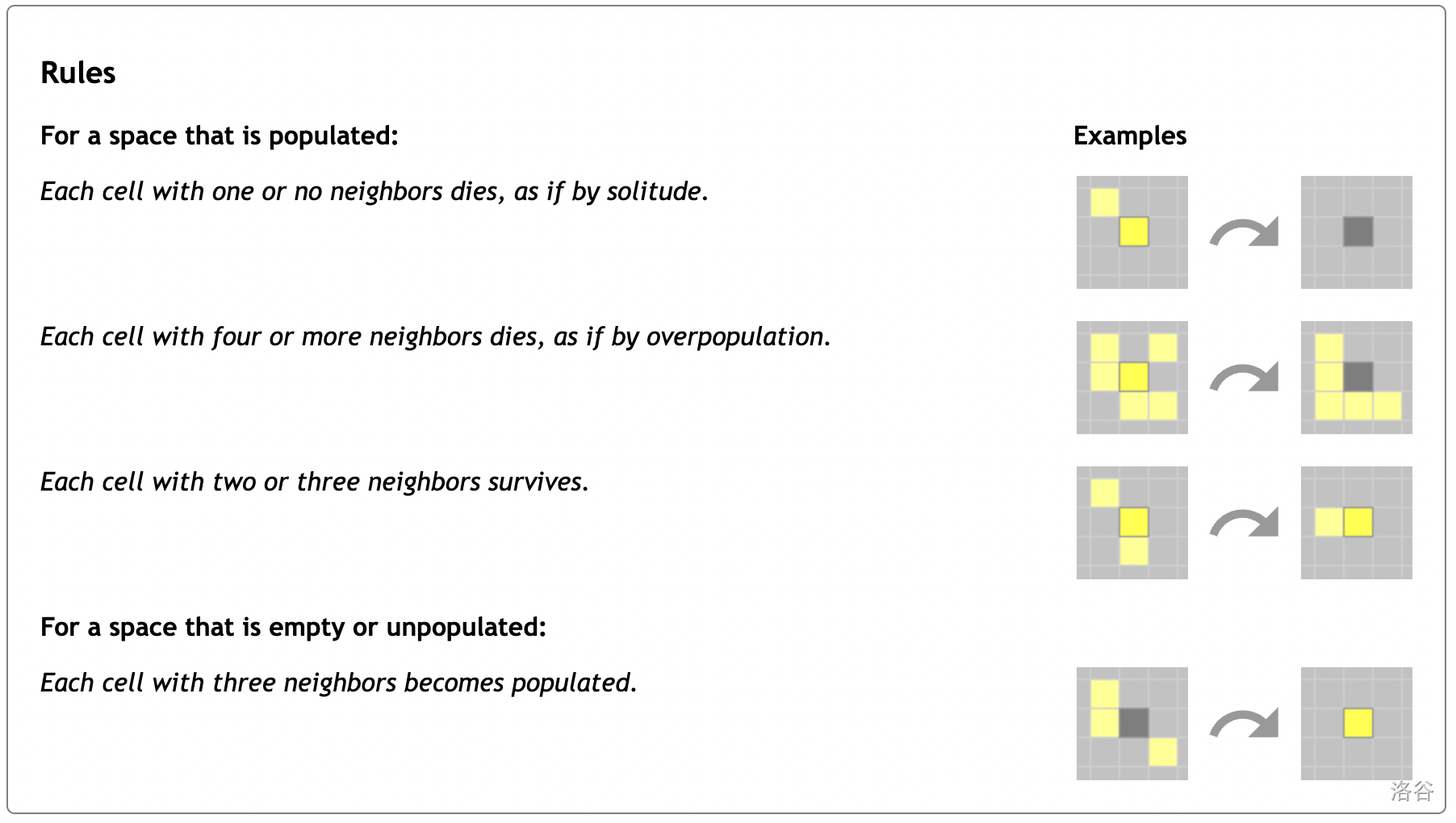   Given an initial configuration, determine the number of live cells after \(k\) iterations.
4. Given an undirected graph with \(n\) vertices and \(m\) edges, each vertex can be colored with one of \(k\) colors. Adjacent vertices (i.e. vertices connected by an edge) must not share the same color. Compute the number of valid colorings modulo \(998244353\).

Important: The input data is provided in an attachment below the problem statement. You must use this input data as supplied.

Note: The first integer in the input will indicate which task you are to solve. Use the corresponding input format described below.

inputFormat

The first integer T (1 ≤ T ≤ 4) specifies which task to solve. The rest of the input depends on the value of T as follows:

• Case 1 (T = 1):
  • A single integer n (1 ≤ n).
• Case 2 (T = 2):
  • Two integers n and m, where there are n vertices on the left and right of the bipartite graph, and m edges.
  • Then follow m lines, each containing two integers u and v (1-indexed). An edge connects the u-th vertex on the left side to the v-th vertex on the right side.
• Case 3 (T = 3):
  • Two integers k and c: k is the number of iterations in Conway's Game of Life, and c denotes the number of live cells initially.
  • Then follow c lines, each with two integers x and y representing the coordinates of an initially live cell.
• Case 4 (T = 4):
  • Three integers: n (number of vertices), m (number of edges), and k (number of colors).
  • Then follow m lines, each containing two integers u and v representing an undirected edge between vertices u and v.

outputFormat

Output a single integer – the answer for the chosen task. For tasks 2 and 4, output the answer modulo \(998244353\).

sample

1
10

3