Realistic Landscape Simulation

The Interactive Creative Players Collective (ICPC) is developing a new computer game that requires realistic landscape generation. An ICPC engineer proposed an algorithm inspired by geological processes. Initially, the landscape is flat, represented by a sequence of n integer height values (from point 1 to point n) all set to 0. A series of modifications are then applied to the landscape using one of the following four operations. Each operation is accompanied by two integers, \(x_1\) and \(x_2\) (with \(x_1 \le x_2\)):

• R (Raise): Increase the height by 1 for all points in the interval \([x_1, x_2]\).
• D (Depress): Decrease the height by 1 for all points in the interval \([x_1, x_2]\).
• H (Hill): Add a hill by increasing heights in a linear shape. Specifically, the heights at \(x_1\) and \(x_2\) are increased by 1. If \(x_2 - x_1 > 1\), then the heights at \(x_1+1\) and \(x_2-1\) are increased by 2. If \(x_2-x_1>3\), the points \(x_1+2\) and \(x_2-2\) are increased by 3, and so on. In general, for any point \(i\) with \(x_1 \leq i \leq x_2\), its height is increased by \(1+\min(i-x_1,x_2-i)\>.
• V (Valley): Add a valley exactly like the hill operation except that the heights are decreased instead.

Your task is to process a sequence of such modifications and output the final landscape as a sequence of integer height values separated by spaces.

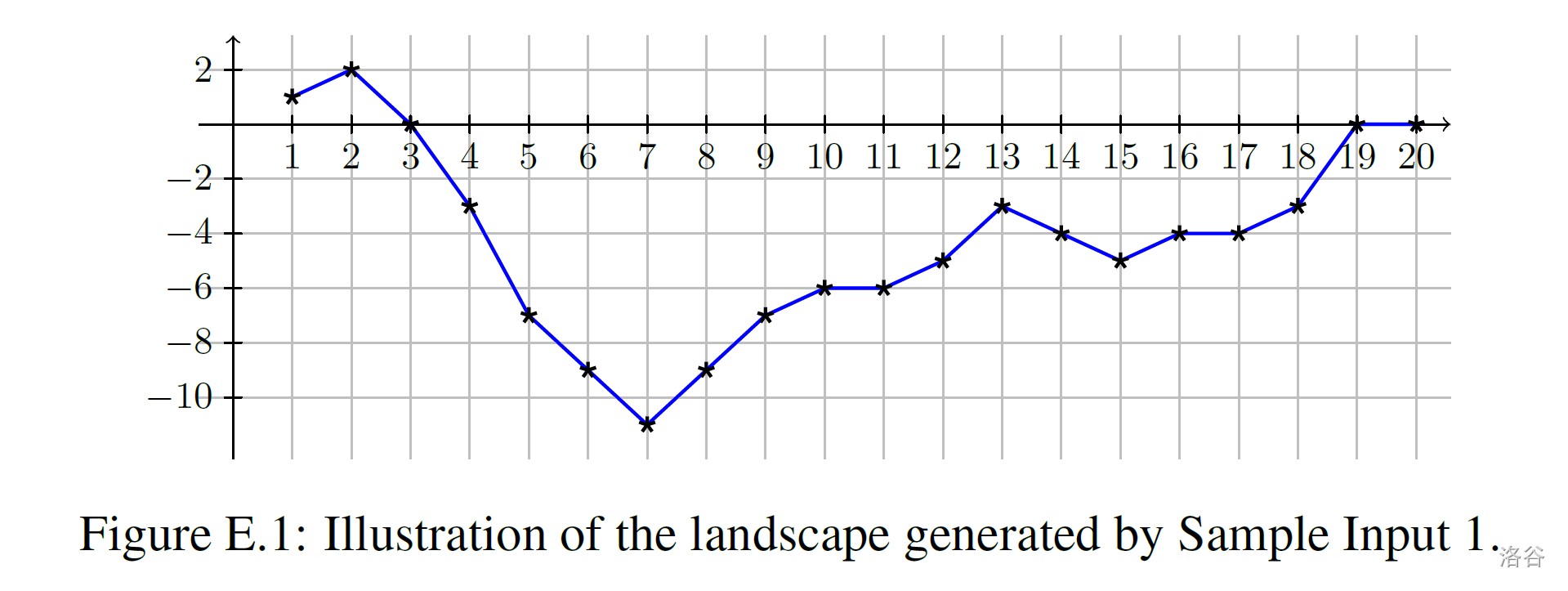
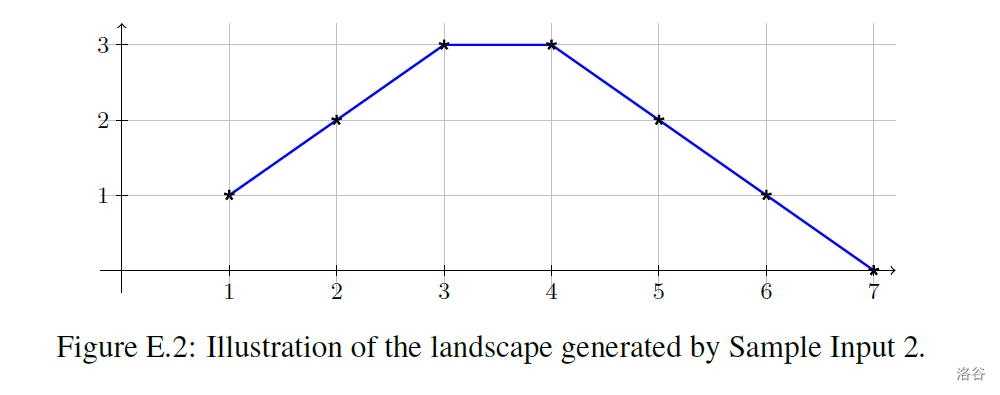
inputFormat

The first line contains two integers \(n\) and \(m\) (n is the number of points in the landscape, and m is the number of modification operations). Each of the following m lines contains an operation in one of the following formats:

• R x1 x2
• D x1 x2
• H x1 x2
• V x1 x2

It is guaranteed that \(1 \le x_1 \le x_2 \le n\).

outputFormat

Output a single line containing \(n\) integers: the final height values (from point 1 to point \(n\)) separated by spaces.

sample

7 3
R 2 5
H 1 7
D 3 4

1 3 3 4 4 2 1