Chandelier Core Merging

The core of the Chandelier can be described as an \( n \times m \) matrix. Initially, every cell of the matrix is an independent space.

If there exist two spaces such that the union of their cells forms a rectangle (i.e. a contiguous submatrix), then these two spaces can be merged into one space (the merged space is exactly the union of the two spaces).

The core reaches a stable state if no two spaces can be merged (i.e. there are no two spaces whose union is a rectangle).

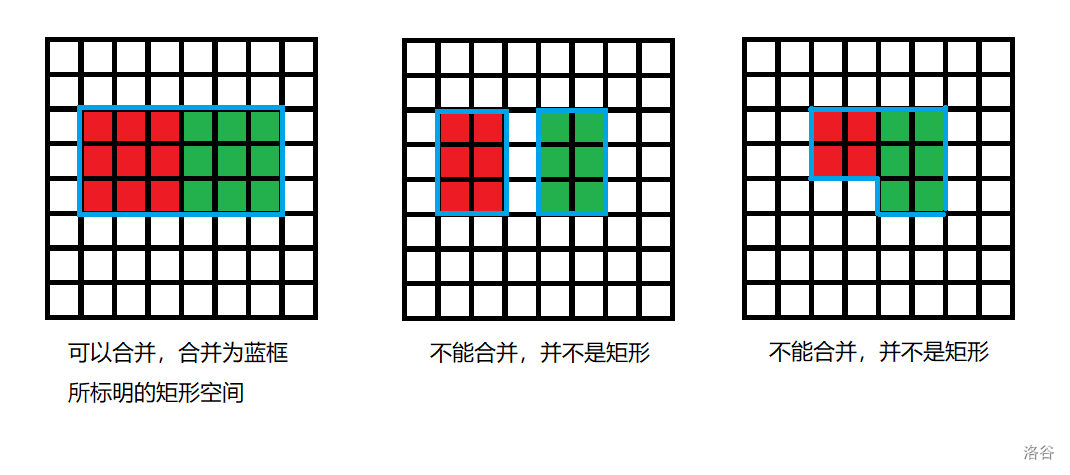
However, if at any point a merged space has a dimension that causes a short circuit, the core will explode. Specifically, if a space's length (the edge parallel to the side of the original matrix of length \(n\)) reaches \(n\) or its width (the edge parallel to the side of length \(m\)) reaches \(m\), then an explosion occurs. Note: The measuring is done with respect to the corresponding edges of the original matrix. That is, if the edge parallel to the \(n\)-side has length \(m\) (with \(m < n\)), then it is considered legal.

Once the core is in a stable state, you can attack and destroy it; the number of attacks required equals the number of remaining spaces. You only have 10 shots available.

Your goal is to control the merging process so that the core reaches a stable state without causing an explosion and with at most 10 remaining spaces. Find one possible final configuration (i.e. a partition of the matrix into spaces) that satisfies these conditions. If it is impossible to achieve a stable, non-explosive state with at most 10 spaces, output -1.

Final configuration format: If possible, output an integer \(k\) (the number of spaces) on the first line, followed by \(k\) lines. Each of the following lines should contain four positive integers \(r_1\), \(c_1\), \(r_2\), \(c_2\) denoting the top-left and bottom-right coordinates (1-indexed) of that space (which is a rectangle). Each space must satisfy:

• height = r2 - r1 + 1 < n (i.e. it does not span all \(n\) rows);
• width = c2 - c1 + 1 < m (i.e. it does not span all \(m\) columns);
• Except that if the side parallel to the \(n\)-side becomes \(m\) (and \(m < n\)), then it is legal.

If no valid configuration exists, simply output -1.

Note: You may assume that \(n, m \ge 1\). In our solution we will treat the cases where \(n < 2\) or \(m < 2\) as unsolvable (i.e. output -1), since any merged space in a 1-row or 1-column matrix would cover the entire row or column.

inputFormat

The input consists of a single line with two integers \(n\) and \(m\) separated by a space.

\(n\) denotes the number of rows and \(m\) denotes the number of columns of the core matrix.

outputFormat

If a valid merging configuration exists, output an integer \(k\) (\(k \le 10\)) on the first line, representing the number of spaces after all merges. Then output \(k\) lines, each containing four integers \(r_1\), \(c_1\), \(r_2\), \(c_2\) which denote the top-left and bottom-right coordinates (1-indexed) of each space.

If no valid configuration exists, output -1.

sample

4 4

4
1 1 2 2
1 3 2 4
3 1 4 2
3 3 4 4

</p>