Alice's Marble Game

Game Description:

Alice is tired of her usual marble game because she always ends in a draw with the computer. To spice things up, Bob invented a new two‐player game played on a diamond board. The board is shaped as shown below:

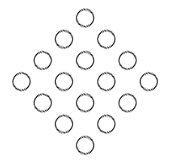
The rules of the game are as follows:

1. The game is played on a diamond board. In our input, the board is described by an integer n (the size of the board) and then 2n-1 rows. The i-th row (1-indexed) contains i characters if i ≤ n and 2n-i characters if i > n. Each character represents a cell: a dot (.) means the cell is empty, and an asterisk (*) means a marble has already been placed.
2. Two players take turns placing marbles. In one move, a player must place between 1 and 3 marbles on empty cells. However, these marbles must be placed consecutively along one straight line among the four possible directions: horizontal, vertical, \(45^\circ\) diagonal, or \(135^\circ\) diagonal. That is, if a player chooses a direction \(d\) and a starting cell, then for some \(L\) with \(1 \le L \le 3\) the cells \[ \text{cell},\; \text{cell}+d,\; \text{cell}+2d,\; \ldots,\; \text{cell}+(L-1)d \] must all be empty and on the board. Examples of legal and illegal moves are illustrated below:
3. If a player has a legal move, they must play; if they cannot place any marble according to the rules, they lose and the other player wins.

Note that Alice always starts the game. In many sessions Alice has played with Bob, but sometimes Bob leaves the game in the middle and hands it over to the computer. The computer always plays optimally. Given the current board state right after Bob’s moves, your task is to determine whether Alice can guarantee a win when playing against the computer.

Input and output details below follow.

inputFormat

Input Format:

• The first line contains an integer n (1 ≤ n ≤ 3), which determines the diamond board size. The board has 2n-1 rows.
• For the i-th row (1-indexed):
  • If i ≤ n, the row contains exactly i characters.
  • If i > n, the row contains exactly 2n-i characters.
  Each character is either . (an empty cell) or * (a cell with a marble).

The board cells are implicitly arranged as a diamond. For the purpose of making moves, the board is embedded in a coordinate system as follows:

• Let the rows be numbered from 0 to 2n-2. For row i, if i < n then it has i+1 cells; otherwise it has 2n-1-i cells.
• Each cell in row i is assigned a coordinate \((x,y)\) where \(y=i\) and \(x = j + offset\) with \(j\) being the 0-indexed position in the row and \(offset = n-1 - \min(i,2n-2-i)\).

Moves: In one move, the current player chooses an empty cell and one of the four directions: horizontal \((1,0)\), vertical \((0,1)\), \(45^\circ\) diagonal \(( -1,1)\), or \(135^\circ\) diagonal \((1,1)\). Then the player places 1 to 3 marbles in that direction in consecutive cells which must all be empty.

outputFormat

Output Format:

Output a single line containing either YES if Alice can guarantee a win against the optimal computer, or NO otherwise.

sample

1
.

YES

</p>