Sum of Maximum Values in Subtriangles

Consider an equilateral triangle of size \(m\) consisting of \(m\) rows, where the \(i\)-th row contains \(i\) numbers. The triangle is arranged in an equilateral (upright) shape. For example, for \(m=4\), the triangle looks like:

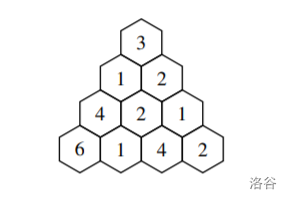
Every such triangle contains many subtriangles. A subtriangle of size \(k\) is defined as follows: if its apex is located at position \((i, j)\) (with \(1 \le i \le m\) and \(1 \le j \le i\)), then the subtriangle of size \(k\) includes row \(i\) (one element), row \(i+1\) (two elements starting from the same column \(j\)), up to row \(i+k-1\) (\(k\) elements). It is required that \(i+k-1 \le m\). Note that every triangle is a subtriangle of itself.

For example, the above \(m=4\) triangle contains:

• 10 subtriangles of size \(1\).
• 6 subtriangles of size \(2\).
• 3 subtriangles of size \(3\).
• 1 subtriangle of size \(4\) (the whole triangle itself).

You are given a triangle of size \(n\) along with an integer \(k\). Your task is to compute the sum of the maximum values within each subtriangle of size \(k\).

Input Format: The first line contains two integers \(n\) and \(k\) (with \(1 \le k \le n\)). The following \(n\) lines describe the triangle. The \(i\)-th line contains exactly \(i\) integers.

Output Format: Output a single integer which is the sum of the maximum values of all subtriangles of size \(k\>.

inputFormat

The first line contains two integers \(n\) and \(k\) separated by a space.

The next \(n\) lines contain the integers of the triangle. The \(i\)-th line has \(i\) space-separated integers.

outputFormat

Output a single integer: the sum of the maximum values in each subtriangle of size \(k\).

sample

4 1
1
2 3
4 5 6
7 8 9 10

55