Minimal Moves to Dismantle n-Chain Puzzle

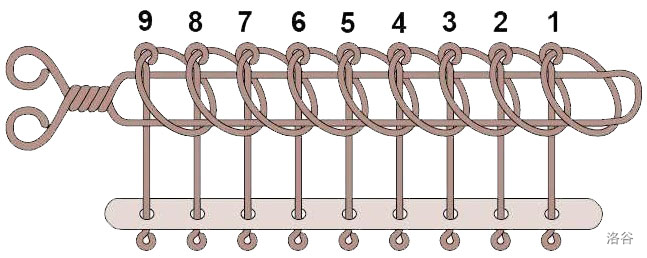
You are given an n‐chain puzzle which has the same structure as the traditional nine-link chain (as shown in the image below). There is a long horizontal bar with n rings hanging on it; note that these rings affect each other in a prescribed manner.

The rings are numbered from 1 to n in order along the bar, with ring 1 at the head of the bar and ring n at the tail. Define f_i as the state of ring i: f_i = 1 means the ring is on the bar while f_i = 0 means it is off the bar. A move (called a dismantle/assemble move) consists of flipping the state of a ring (i.e. 1 becomes 0, and 0 becomes 1).

The legal moves are governed by the following rules:

1. Ring 1 can be flipped at any time, independently.
2. For k ≥ 1, ring k+1 can be flipped individually if and only if f_k = 1 and for all i < k we have f_i = 0.
3. If f₁ = f₂, then rings 1 and 2 can be flipped together in a single move.

Your task is: Given the initial state of the n-chain, compute the minimum number of moves required to completely dismantle the chain (i.e. make all f_i = 0).

inputFormat

The input consists of two lines.

• The first line contains a single integer n (the number of rings).
• The second line contains n integers, each being either 0 or 1, representing the initial states f₁, f₂, ..., f_n (1 indicates the ring is on the bar and 0 indicates it is off the bar).

outputFormat

Output a single integer: the minimum number of moves required to achieve the state where all rings are off the bar (i.e. all f_i = 0).

sample

1
1

1