Camel Tour

We define a new chess piece called the camel chess piece. Its movement rules are as follows:

• You can move it horizontally or vertically such that there are exactly 2 cells between the old and new positions (i.e. a jump of 3 cells in that direction).
• Alternatively, you can move it diagonally such that there is exactly 1 cell between the old and new positions (i.e. a jump of 2 cells diagonally).

The diagram below illustrates a camel chess piece at the center with the 8 possible destination cells marked with an x:

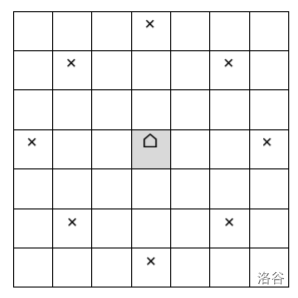
The board is an N × N grid where N is guaranteed to be divisible by 5. Initially the piece is placed at the top‐left corner of the board. A camel cycle is defined as a sequence of moves such that:

• Every cell of the board is visited exactly once, and
• The final cell is a valid camel move away from the starting cell.

Your task is to find a camel cycle for a given board or determine that none exists.

inputFormat

The input consists of a single integer N (5 | N) representing the dimension of the board.

outputFormat

If a camel cycle exists, output N lines, each containing N space‐separated integers which represent the order in which the cells are visited (starting from 1). Otherwise, output -1.

sample

5

A valid 5x5 board listing a camel cycle (for example, one possible output is shown below, though your program may output any valid cycle):
14 21  4  9 18
5 10 19 12  1
20  3 16  7 13
11  6 15  8 17
2 23  0  ?  ?
(Note: The output must represent a valid cycle where the last cell can jump back to the first cell via a camel move.)