Festive Binary Search Tree

To celebrate the New Year, Farmer John has decided to give his cows a festive binary search tree! Starting with a permutation \(a = \{1,2,\dots,N\}\), he constructs a binary search tree using the following pseudo‐code:

generate(l, r):
  if l > r, return empty subtree;
  x = \(\arg\min_{l \le i \le r} a_i\);  // index of the minimum element in \(\{a_l,\dots,a_r\}\)
  return a BST with a[x] as the root, 
    generate(l, x-1) as the left subtree, and
    generate(x+1, r) as the right subtree;

For example, the permutation \(\{3,2,5,1,4\}\) produces the BST shown below:

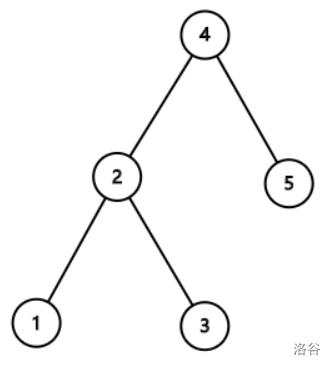
Let \(d_i(a)\) denote the depth of node \(i\) (i.e. the node with value \(i\)) in the BST formed by permutation \(a\); here the depth is defined as the number of nodes in the path from that node to the root. In the above example, \(d_4(a)=1,\; d_2(a)=d_5(a)=2,\; d_1(a)=d_3(a)=3\).

We say a permutation \(a\) has \(K\) inversions if the number of pairs \((i,j)\) satisfying \(1 \le i a_j\) equals \(K\). It is known that Farmer John’s permutation \(a\) used to generate the BST has exactly \(K\) inversions. For all such permutations, please compute for each \(1 \le i \le N\) the value of

\[ \sum_{a \text{ with exactly } K \text{ inversions}} d_i(a) \mod M, \]

and output the results for \(i=1,2,\dots,N\).

inputFormat

The first and only line contains three integers \(N, K, M\) where \(N\) is the size of the permutation, \(K\) is the required number of inversions, and \(M\) is the modulus.

outputFormat

Output a single line containing \(N\) integers. The \(i\)-th integer should be the sum of depths \(d_i(a)\) over all permutations \(a\) with exactly \(K\) inversions, taken modulo \(M\).

sample

3 0 100

1 2 3

</p>