Maximum Root-to-Leaf Path Sum in a Chino Tree

A Chino Tree is a special kind of full binary tree with the following property:

• For every non-leaf node, let its left child be A and its right child be B. Then the right child of A (denoted as C) and the left child of B (denoted as D) have the same value, and the subtrees rooted at C and D are identical.

Given such a tree where every node has an associated weight, your task is to compute the maximum sum of weights along a path from the root to any leaf. The tree is a perfect binary tree (i.e. every non-leaf node has exactly two children and all leaves are at the same depth).

The input provides the height h of the tree (with 1 ≤ h ≤ 20), and then the node weights in level order. The total number of nodes is 2^h - 1.

Your solution should output the maximum sum of weights from the root to any leaf.

The following diagram illustrates an example tree:

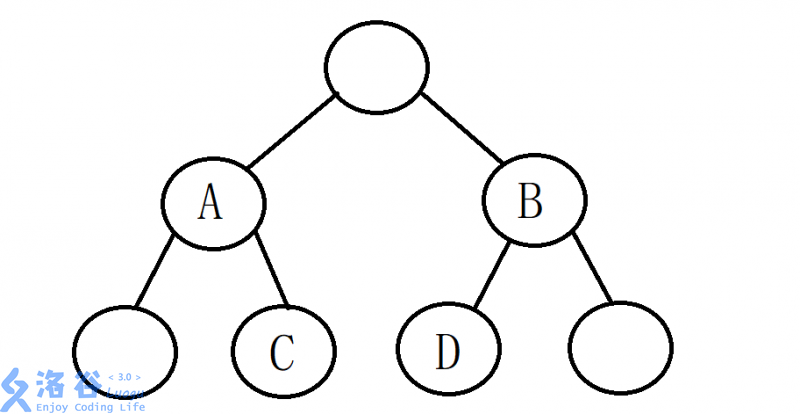
Note: All formulas must be represented in LaTeX format. For instance, the condition for the two children is given by: $$C = D$$ and the corresponding subtrees are identical.

inputFormat

The first line of input contains a single integer h representing the height of the tree.

The second line contains 2^h - 1 space-separated integers representing the weights of the nodes in level order.

Example:

3
1 2 3 4 5 6 7

outputFormat

Output a single integer: the maximum sum of weights from the root to any leaf.

Example:

11

sample

2
1 2 3

4

</p>