Minimum Covering Double Circle

Given n points in the plane \( (x_1, y_1), (x_2, y_2), \ldots, (x_n, y_n) \), find two circles \( R_1 \) and \( R_2 \) of equal radius such that every point is covered by at least one of these circles and the radius is minimized.

In other words, determine the smallest \( r \) such that there exist two circles of radius \( r \) covering all the given points. The problem can be mathematically formulated as follows:

Find the minimum \( r \) for which there exist two circles \( R_1 \) and \( R_2 \) with radius \( r \) that satisfy \[ \{(x_i, y_i)\}_{i=1}^n \subseteq R_1 \cup R_2, \] where each circle \( R_j \) is defined by \[ R_j = \{ (x,y) \mid (x - a_j)^2 + (y - b_j)^2 \le r^2 \}, \quad j=1,2. \]

The sample diagram below illustrates the two circles covering the points:

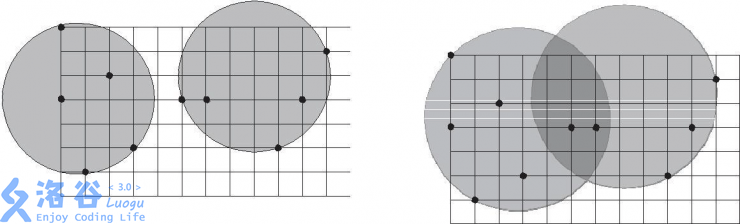
inputFormat

The first line contains an integer \( n \) denoting the number of points.

Each of the next \( n \) lines contains two real numbers \( x_i \) and \( y_i \) representing the coordinates of a point.

outputFormat

Output a single real number representing the minimal radius \( r \). The answer is accepted if it is correct within an absolute or relative error of \(10^{-6}\).

sample

1
0 0

0.000000