Graph Connectivity Count

Given a directed graph, we define the connectivity count as the number of ordered vertex pairs \((u,v)\) such that there exists a path from vertex \(u\) to vertex \(v\). Note that each vertex is always reachable from itself.

For example, consider the following graph:

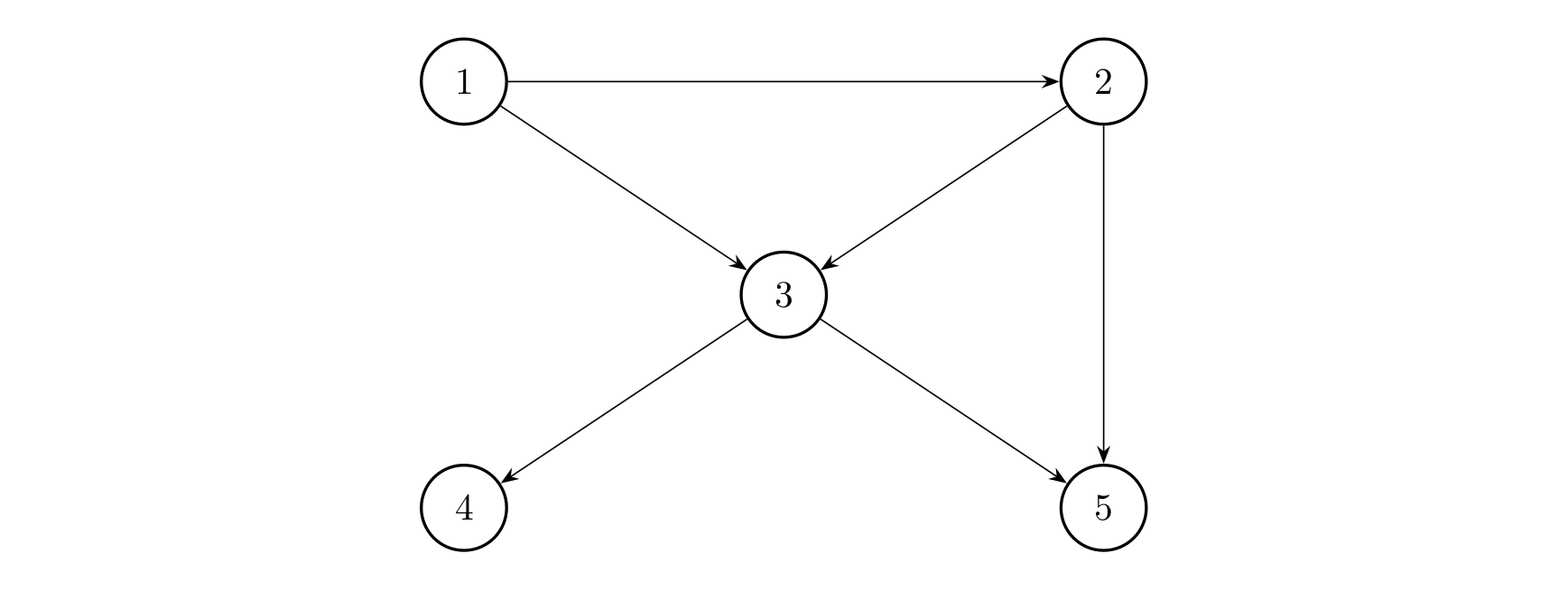
• Vertex \(1\) can reach \(\{1,2,3,4,5\}\)
• Vertex \(2\) can reach \(\{2,3,4,5\}\)
• Vertex \(3\) can reach \(\{3,4,5\}\)
• Vertices \(4\) and \(5\) can only reach themselves

The connectivity count for this graph is \(5+4+3+1+1=14\).

Your task is to compute the connectivity count for a given directed graph.

inputFormat

The first line contains two integers (n) and (m), representing the number of vertices and edges respectively. (1 \leq n \leq 10^5) and (0 \leq m \leq 10^5). Each of the next (m) lines contains two integers (u) and (v), indicating there is a directed edge from vertex (u) to vertex (v). Vertices are numbered from (1) to (n).

outputFormat

Output a single integer: the connectivity count of the graph.

sample

5 9
1 2
1 3
1 4
1 5
2 3
2 4
2 5
3 4
3 5

14