Chessboard Horse Jump

Given a chessboard with (n) rows and (m) columns, a horse starts at the top-left cell ((1,1)) and wishes to reach the bottom-right cell ((n,m)). The horse moves according to the following rules:

1. In each move, it jumps to the right by an odd number of columns (i.e. (1, 3, 5, \ldots)).
2. It can land in the same row or an adjacent row (i.e. one row above or below), but during the jump the horse must remain within the boundaries of the board.

For example, when (n = 3) and (m = 10), one valid sequence of jumps is illustrated below:

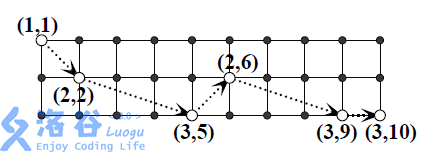
Your task is to compute the number of valid jump sequences modulo (30011).

inputFormat

The input consists of a single line containing two integers (n) and (m) ((1 \leq n, m \leq 1000)), representing the number of rows and columns of the chessboard, respectively.

outputFormat

Output a single integer: the number of valid jump sequences from the top-left to the bottom-right cell, taken modulo (30011).

sample

3 10

1863