Binary Tree Metrics

Given a binary tree in which each node is numbered from 1 to n with node 1 as the root, you are to calculate three metrics:

• The depth of the tree, i.e. the maximum number of nodes on any root‐to‐leaf path. In other words, if the root is at level 1 then the depth is the maximum level of any node.
• The width of the tree, defined as the maximum number of nodes across any level of the tree.
• The distance from a given node x to another given node y.

The tree is an ordinary binary tree; however, its edges are naturally directed from parent to child. When computing the distance from node x to node y, you are allowed to traverse edges in the reverse direction (i.e. from child to parent). Traversing an edge with the arrow (from parent to child) costs 1; traversing an edge against the arrow (from child to parent) costs 2.

Thus, if you take the unique path from x up to the lowest common ancestor (LCA) of x and y and then down to y, the distance is defined as

$\text{distance}(x,y)=2\times (\text{number of upward moves from } x \text{ to } LCA) + (\text{number of downward moves from } LCA \text{ to } y)$

For example, consider the binary tree below:

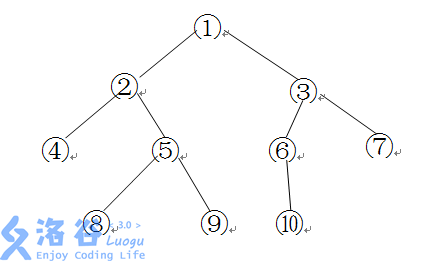
• Depth: $4$
• Width: $4$
• Distance from node $8$ to node $6$: $8$
• Distance from node $7$ to node $6$: $3$

You are given a binary tree described below and two designated nodes x and y. Compute the tree's depth, its maximum width, and the distance from x to y as defined above.

inputFormat

The input consists of multiple lines:

1. The first line contains three integers: n x y, where n is the number of nodes in the tree, and x and y are two designated nodes.
2. The next n lines each contain two integers representing the indices of the left and right children of node i (for i from 1 to n). A value of -1 indicates that the child does not exist.

It is guaranteed that the tree is valid and that node 1 is the root.

outputFormat

Output three integers separated by a space:

• The depth of the tree.
• The maximum width of the tree (i.e. the maximum number of nodes at any level).
• The distance from node x to node y computed as defined: if the lowest common ancestor (LCA) of x and y is at depth d, and x and y are at depths d_x and d_y respectively, then the distance is 2*(d_x - d) + (d_y - d).

sample

8 8 6
2 3
7 6
4 5
8 -1
-1 -1
-1 -1
-1 -1
-1 -1

4 4 8