Maximizing the Matchstick Number

Fish, a sea‐dwelling fish, spent a boring day collecting human litter – matchsticks – and arranged them to form a decimal number with n digits. Each digit is formed using a fixed pattern of matchsticks. For example, the digit 1 is formed with 2 matchsticks; the other digits are formed as shown in the figures below:

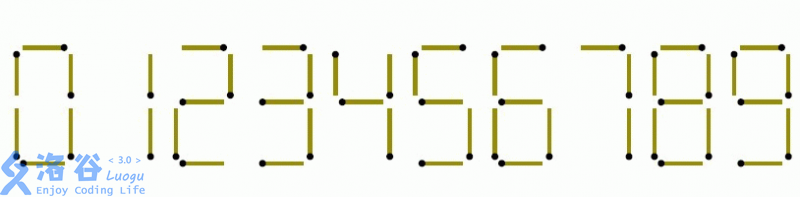
Exhausted after the work, Fish was unhappy with the number he had formed. He decided to re-arrange some of the matchsticks in order to make the number as large as possible. However, he can move at most k matchsticks. Note that he is not allowed to break any stick or simply discard one. Also, because the lowest–order digit is fixed against a wall, he cannot add a new digit at the right end; he may only add new digits to the left (i.e. as a prefix).

For each digit you choose to form, you must use exactly the number of matchsticks prescribed by that digit. The number of matchsticks required for each digit is given below:

• 0,6,9: 6 matchsticks
• 1: 2 matchsticks
• 2,3,5: 5 matchsticks
• 4: 4 matchsticks
• 7: 3 matchsticks
• 8: 7 matchsticks

When a digit is transformed, the cost in moves is equal to the absolute difference in the number of matchsticks used. In other words, if a digit originally uses a matchsticks and you want to change it to a digit that uses b matchsticks, you must move |b - a| matchsticks. For a new digit that is added (which starts with 0 matchsticks) the cost is exactly the number of matchsticks needed (for example, to add the digit 9 you must spend 6 moves).

Your goal is to obtain the maximum possible decimal number by reassigning at most k matchsticks among the n original digits and (optionally) new digits added to the front of the number. The final number is obtained by concatenating the new digits (if any) with the transformed original n-digit number. Note that even if a matchstick is moved from a digit (thereby reducing its matchstick count) to be added to some other digit, that move counts exactly once. Moreover, all moves are independent – you may choose to leave some original digits unchanged (incurring 0 moves) or change them by moving some matchsticks.

For clarity, the minimal move cost for transforming a digit d (with s(d) matchsticks) into a digit c is:

$$cost = |s(c) - s(d)|,$$

and for forming a new digit c (from scratch) the cost is:

$$cost = s(c).$$

You may assume that Fish always uses a valid initial configuration. Help him compute the maximum number he can obtain under these operations.

inputFormat

The first line contains two integers n and k (1 ≤ n ≤ 105, 0 ≤ k ≤ 109) -- the length of the original number and the maximum number of matchsticks that can be moved, respectively.

The second line contains a string of n digits representing the original number (which is a valid configuration according to the digit patterns).

outputFormat

Output the maximum possible number (as a string) that can be obtained by moving at most k matchsticks.

sample

1 3
1

71

</p>