Perimeter of the Covered Region

There are n circular discs falling from the sky in sequence. A later disc can cover parts of the earlier ones. After all discs have fallen, a closed region is formed whose boundary is the union of the visible parts of the discs. Your task is to compute the total perimeter of this closed region. In other words, sum the lengths of all the red boundary arcs shown in the figure below.

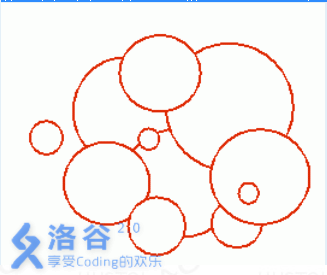
Note that if a disc is partially covered by a later disc, only the uncovered portion of its circumference contributes to the final perimeter. If a disc is completely covered by a later one, it does not contribute at all.

The arc length contributed by a disc with radius r is given by
\( \text{arc length} = r \times \theta \),
where \( \theta \) is the uncovered angle (in radians).

For two discs with centers \( (x_i,y_i) \) and \( (x_j,y_j) \) and radii \( r_i \) and \( r_j \) respectively, if disc j (which falls later than disc i) covers a part of disc i, then let \( d \) be the distance between the centers. If \( d < r_j + r_i \) and disc j does not completely cover disc i (i.e. \( d > r_j - r_i \)), the covered arc on disc i will subtend an angle of
\( 2 \alpha \) where \( \alpha = \arccos\Big(\frac{d^2 + r_i^2 - r_j^2}{2 r_i d}\Big) \).

inputFormat

The input begins with an integer n (the number of discs).

Each of the next n lines contains three floating-point numbers x, y, and r, representing the x-coordinate, y-coordinate of the center, and the radius of a disc, respectively. The discs are given in the order they fall (from first to last).

Constraints:
1 ≤ n ≤ 1000;
All coordinates and radii are positive and do not exceed 10⁴.

outputFormat

Output a single real number, which is the total perimeter of the closed region formed by the visible parts of all discs. The answer should be rounded to three decimal places.

sample

1
0 0 1

6.283