Gemstone Commemorative Coins

Constantine has just finished his vacation on MySky Island and is about to leave. Before he departs, he wishes to give his dear friend YY a special gift – a handcrafted gemstone commemorative coin made on MySky Island. One side of the coin is engraved with the island's name, "MySky", or with the recipient’s name, for example, "to YY". The other side of the coin is inlaid with a circle of n colored gemstones, arranged evenly along the edge. For example, when n = 7 the layout might look like this:

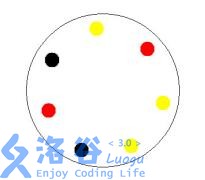
Because the coin is circular, two color arrangements that can be matched by a rotation are considered identical. Note: Since only one side of the coin is inlaid with gemstones, if two arrangements become identical after a flip (reflection) they are considered the same; however, if they can only be made identical by rotation (and not by reflection alone), they are considered different arrangements.

According to the local custom on MySky Island, a coin must have an odd number of gemstones, as an even number is believed to be unlucky. The coins are made on site and visitors may choose the colors of the gemstones. Constantine has selected his 17 favorite colors (since 17 is his lucky number) and now wonders: if he makes sure that every one of these 17 colors appears at least once, how many different commemorative coins can be produced?

The answer may be very large. You only need to output the last 120 digits of the answer. All formulas in this description are given in \( \LaTeX \) format. In particular, one way to express the answer is:

[ \text{Answer} = \frac{1}{n} \sum_{d|n} \varphi(d) \left( \sum_{j=0}^{17} (-1)^j \binom{17}{j} (17-j)^{\frac{n}{d}} \right), ]

where \( \varphi(d) \) is Euler's totient function. Two arrangements are considered the same if one can be rotated to match the other.

inputFormat

The input consists of a single line containing an odd integer n (n \ge 17), which represents the number of gemstones in the coin.

outputFormat

Output the last 120 digits of the number of distinct commemorative coins that can be formed (using all 17 colors at least once) under rotational equivalence. If the resulting number has fewer than 120 digits, print the number normally.

sample

17

EXPECTED_OUTPUT_FOR_17