Magic Square Arrangement

You are given an n × n grid (matrix) and n × n integers. Your task is to fill the grid with these integers (each integer must be used exactly once) so that the sum of the numbers in each row, each column, and each of the two main diagonals are equal.

More precisely, if the filled grid is denoted as \(a_{ij}\) for \(1 \le i,j \le n\), you must have:

[ \sum_{j=1}^{n}a_{ij}=S \quad (\text{for every row } i), ]

[ \sum_{i=1}^{n}a_{ij}=S \quad (\text{for every column } j), ]

[ \sum_{i=1}^{n}a_{ii}=S \quad \text{and} \quad \sum_{i=1}^{n}a_{i,n+1-i}=S, ]

It is guaranteed that there exists at least one arrangement for the given input. Below are a few examples:

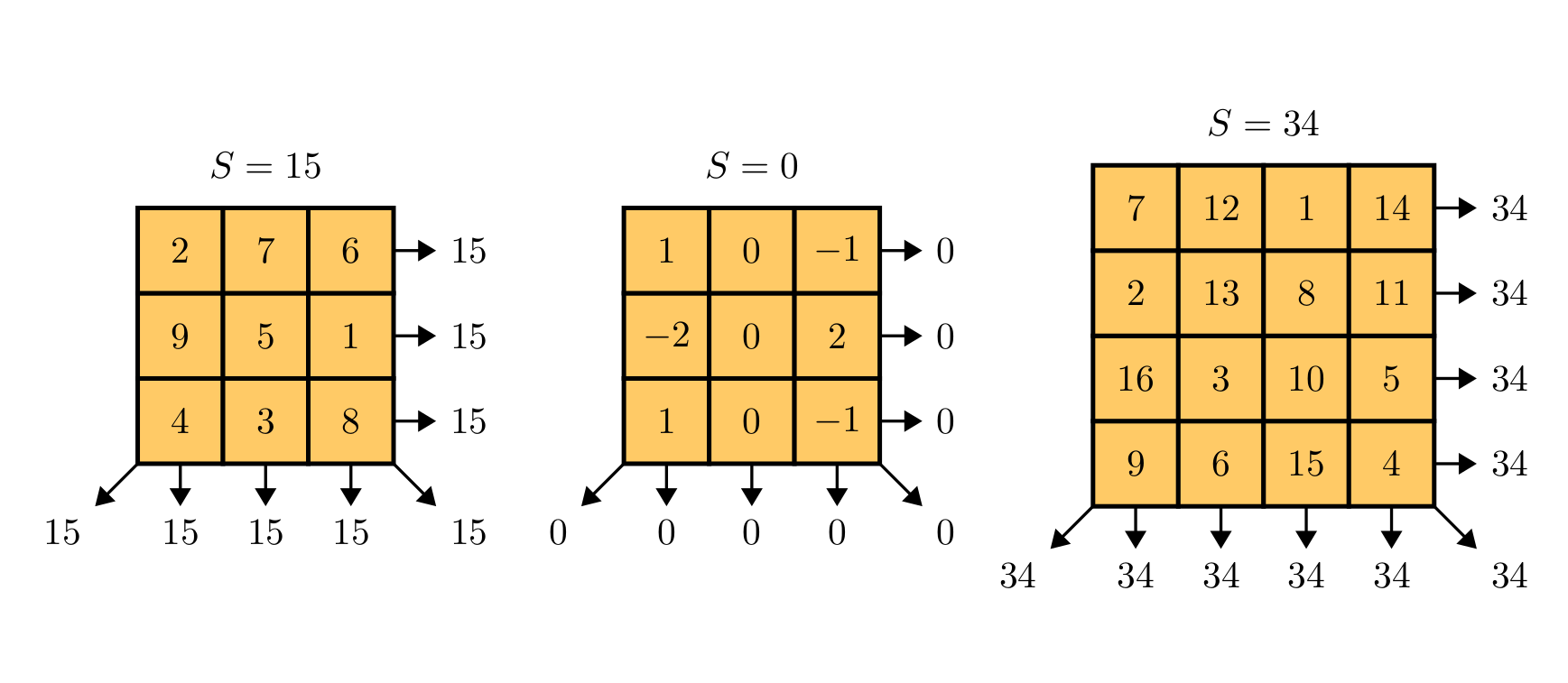
inputFormat

The first line contains an integer n (the dimension of the matrix). The second line contains n × n integers separated by spaces.

Example:

3
2 7 6 9 5 1 4 3 8

outputFormat

Output the filled matrix in n lines. Each line should contain n integers separated by a single space, representing a valid arrangement where each row sum, column sum, and the sums of the two diagonals equal the same constant.

If no valid solution exists, output -1. (For this problem, a valid solution is guaranteed for the given input.)

sample

3
2 7 6 9 5 1 4 3 8

2 7 6
9 5 1
4 3 8