6 Queens Problem

Given a 6 × 6 board, place 6 pieces on the board so that there is exactly one piece in each row and each column, and at most one piece on every diagonal (including all diagonals parallel to both main diagonals). Such an arrangement can be represented by a sequence.

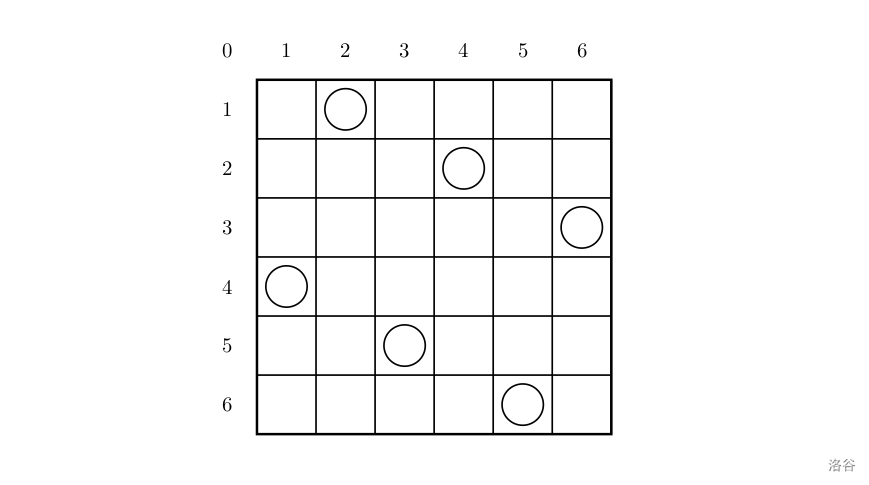
For example, the layout shown below can be represented by the sequence \(2\ 4\ 6\ 1\ 3\ 5\), where the \(i\)th number indicates that in row \(i\) the piece is placed in column given by that number:

• Row numbers: 1, 2, 3, 4, 5, 6
• Column numbers: 2, 4, 6, 1, 3, 5

This is only one valid placement. Write a program to find all valid placements of the pieces. Output the solutions using the sequence representation as above, and list the solutions in lexicographical (dictionary) order.

Print the first 3 solutions, each on one line. In the last line, output the total number of solutions.

Note: All mathematical formulas must be formatted in \(\LaTeX\) format.

inputFormat

This problem does not require any input.

None

outputFormat

Output the first 3 lexicographically smallest valid sequences representing the placements. Each sequence should be printed on a separate line with a space separating the numbers. In the last line, output the total count of valid solutions.

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4

sample

2 4 6 1 3 5
3 6 2 5 1 4
4 1 5 2 6 3
4