Counting 8-Shaped Figures

Two circles on a plane form an 8-shaped figure if they touch each other but neither lies inside the other. In this problem, the only possible way for two circles to touch under the given constraints is to have exactly one common point. Formally, two circles with centers \((x_1,y_1)\) and \((x_2,y_2)\) and radii \(r_1\) and \(r_2\) are externally tangent if and only if

where \(d = \sqrt{(x_1-x_2)^2+(y_1-y_2)^2}\) is the distance between the centers. Note that if two circles touch each other internally, then one would lie inside the other, which is not allowed for an 8-shaped figure.

You are given a collection of \(n\) circles on the plane. No two circles intersect at more than one point. Your task is to determine the number of pairs of circles that form an 8-shaped figure.

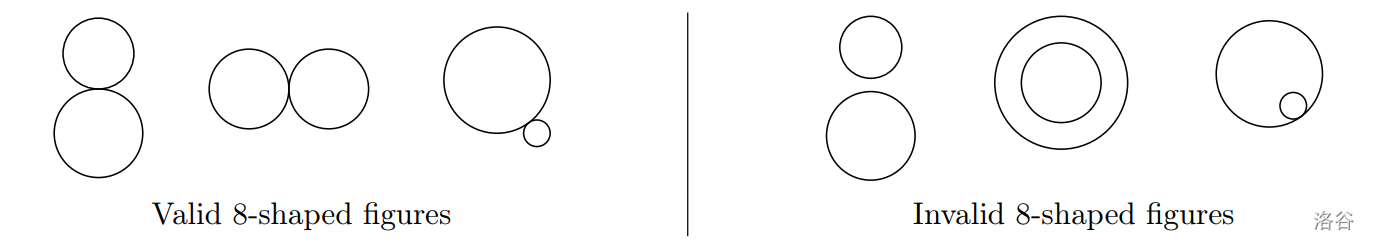
inputFormat

The first line contains an integer \(n\) (\(1 \le n \le 10^5\)), representing the number of circles.

Each of the following \(n\) lines contains three integers \(x\), \(y\), and \(r\), denoting the center coordinates and the radius of a circle. It is guaranteed that no two circles intersect in more than one point.

outputFormat

Output a single integer representing the number of pairs of circles that form an 8-shaped figure.

sample

3
0 0 1
2 0 1
0 3 2

1