Translation Congruent Convex Hull Areas

Let \(S_1\) and \(S_2\) be two finite sets of points in the plane. For any non‐empty subsets \(T_1 \subseteq S_1\) and \(T_2 \subseteq S_2\), denote by \(\operatorname{Conv}(T_1)\) and \(\operatorname{Conv}(T_2)\) their convex hulls. It is guaranteed that both convex hulls have a positive area. Moreover, we say that two convex polygons \(P\) and \(Q\) coincide up to translation if there exists a two‐dimensional vector \(\mathbf{v}\) such that

[ P \in \operatorname{Conv}(T_1) \iff P+\mathbf{v} \in \operatorname{Conv}(T_2), ]

In other words, \(\operatorname{Conv}(T_1)\) and \(\operatorname{Conv}(T_2)\) are identical after a translation. Your task is to find all possible areas of \(\operatorname{Conv}(T_1)\) for which there exists some corresponding subset \(T_2 \subseteq S_2\) with \(\operatorname{Conv}(T_2)\) translation–equivalent to \(\operatorname{Conv}(T_1)\).

Note: Two convex polygons are translation–congruent if and only if their shapes (i.e. the cyclic list of edge vectors) are identical. In our solution such a polygon is represented by the ordered sequence of its edge vectors (which is invariant under translation up to a cyclic rotation). Moreover, all areas should be output with one digit after the decimal point.

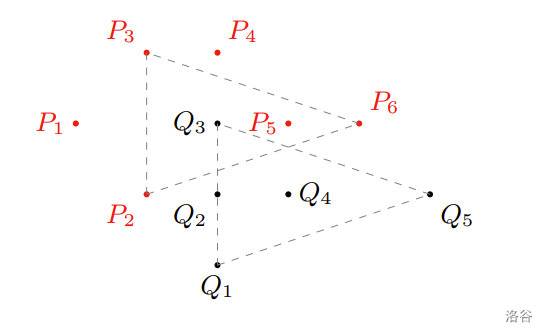
Below is an illustration of two convex hulls that coincide up to translation.

inputFormat

The input begins with a line containing two integers \(n_1\) and \(n_2\) \( (3 \le n_1, n_2 \le 10)\) denoting the number of points in \(S_1\) and \(S_2\) respectively.

The next \(n_1\) lines each contain two integers representing the coordinates of the points in \(S_1\). The following \(n_2\) lines each contain two integers for the coordinates of the points in \(S_2\).

You may assume that all points have integer coordinates and that no three points of a chosen subset are collinear if the convex hull is to have positive area.

outputFormat

Output a single line containing all distinct possible areas (of \(\operatorname{Conv}(T_1)\)) in increasing order, separated by a single space. Each area must be rounded to one decimal place. If no valid convex hull exists (although this will not occur in the input), output an empty line.

sample

4 4
0 0
0 1
1 0
1 1
1 1
1 2
2 1
2 2

0.5 1.0