Counting Valid Rectilinear Polygons

You are given two integers N and K. Consider the Cartesian coordinate system with integer lattice points \((x,y)\) satisfying \(0 \le x \le N\) and \(0 \le y \le K\). A rectilinear polygon is defined as a closed simple polygon whose vertices are some of these lattice points and each edge is either horizontal or vertical. Furthermore, the polygon’s boundary is a closed curve that does not touch or cross itself except at consecutive endpoints. Note that two polygons with the same shape but placed in different positions are considered different.

For example, the following is a valid polygon:

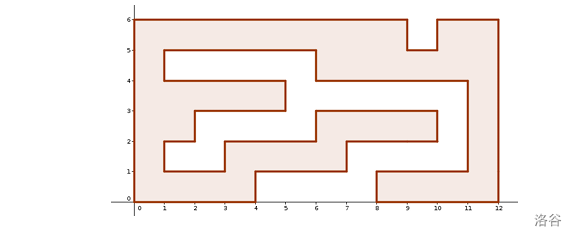
While the following are not valid:

Your task is to count the total number of valid rectilinear polygons among the lattice points. It is guaranteed that the input values will be small so that a brute‑force search is feasible.

Note: A polygon must have at least 4 vertices. In order to avoid counting the same polygon more than once (when rotated or translated), you should only count a polygon if its lexicographically smallest vertex is chosen as the starting point during enumeration.

Input Formula: Two integers N and K

Output Formula: A single integer representing the number of valid polygons.

inputFormat

The first and only line of input contains two integers N and K separated by a space, where \(0 \le N, K \le 3\).

outputFormat

Output a single integer — the number of valid rectilinear polygons satisfying the above conditions.

sample

1 1

1