Matchstick Equations

You are given n matchsticks. Using all of them, you need to form an equation of the form $$A+B=C$$ where each of A, B and C is a non‐negative integer that is represented by matchsticks. The digits from 0 to 9 are formed with matchsticks as shown in the figure below (each digit has a fixed matchstick cost):

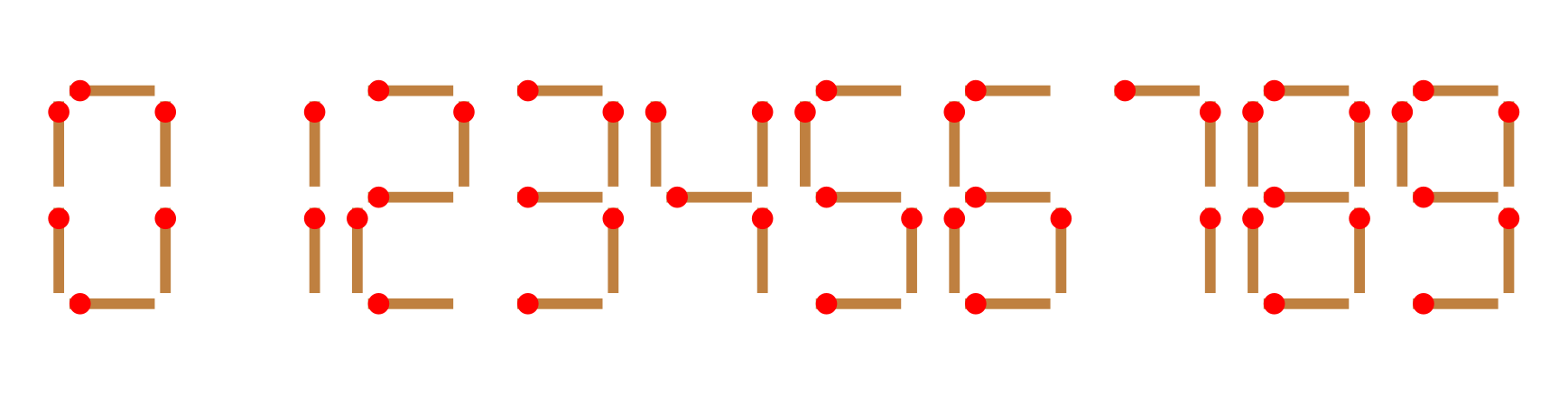
Note that:

1. The plus sign and the equals sign each require 2 matchsticks.
2. If A ≠ B, then the equations A+B=C and B+A=C are considered different.
3. If a number is not zero, its representation cannot have leading zeros. (The only allowed representation for 0 is "0".)
4. All n matchsticks must be used.

Each digit has the following matchstick cost (in matches):

• 0: 6 matches
• 1: 2 matches
• 2: 5 matches
• 3: 5 matches
• 4: 4 matches
• 5: 5 matches
• 6: 6 matches
• 7: 3 matches
• 8: 7 matches
• 9: 6 matches

The plus sign and equals sign together consume 4 matchsticks. Let $$S=n-4$$ be the number of matchsticks available to form the three numbers. Count the number of distinct equations $$A+B=C$$ that can be made so that the total matchstick cost used to form the digits of A, B and C is exactly $$S$$. In the equation, the addition is performed in the usual way (digit‐by‐digit addition with possible carries).

Input/Output requirement: The input consists of a single integer n (with n ≥ 4) and the output should be a single integer representing the number of valid equations.

Note on representation: When a number has more than one digit its highest (most significant) digit cannot be 0. For example, if a number is 0 it must be represented as "0" and not "00" or "000".

inputFormat

The input consists of a single line containing one integer n (n ≥ 4), which is the total number of matchsticks.

outputFormat

Output a single integer, which is the number of expressions of the form A+B=C that use exactly n matchsticks.

sample

18

1