Beauty of Fireworks

We are given a rooted tree (T^1) with (n) nodes. The tree (T^m) is defined recursively as follows: for each leaf of (T^{m-1}), attach a copy of (T^1) (by connecting its root to the leaf) to obtain (T^m). An illustration is shown below:

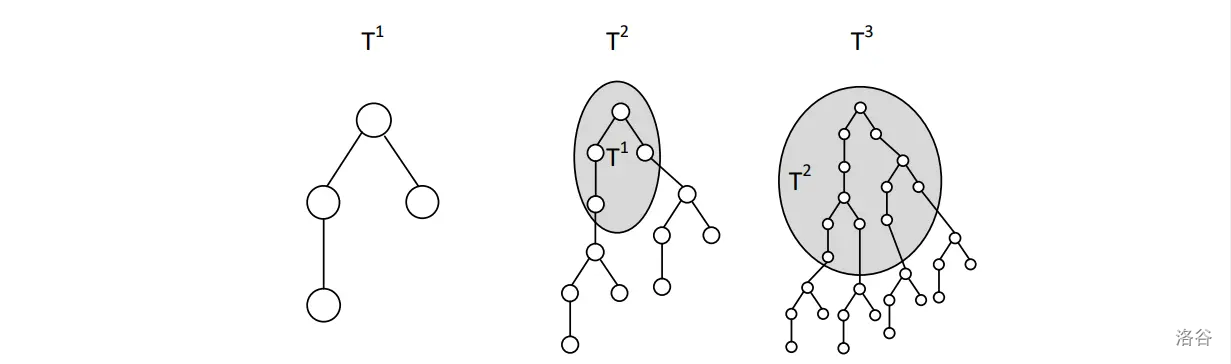
Your task is to compute the length (i.e. the number of nodes) of the diameter of (T^m). Recall that the diameter of a tree is the longest simple path in the tree. It is known that in any tree the endpoints of a diameter are always leaves. In our problem, let (D) denote the diameter (in (T^1), measured in nodes). It can be shown that the diameter of (T^m) is given by [ \mbox{diam}(T^m) = m\cdot D - (m-1). ]

For example, if (T^1) is a chain of (n) nodes then (D=n) and (\mbox{diam}(T^m)= m,n - (m-1)). If (T^1) is a star (with center and leaves) then (D=3) and for (m=2) the diameter is (2\cdot 3-1 = 5). Your program should implement this computation.

All formulas above are in LaTeX format.

inputFormat

The input consists of two parts:

1. The first line contains two integers (n) and (m) (with (n \ge 1) and (m \ge 1)).
2. If (n > 1), the second line contains (n-1) integers. The (i)-th integer (for (i = 1, 2, \ldots, n-1)) denotes the parent of node (i+1) in (T^1) (nodes are numbered from 1 to (n), and node 1 is the root). If (n = 1), the second line is omitted.

outputFormat

Output a single integer – the number of nodes on the diameter of (T^m).

sample

1 3

1