Maximum Signal Distance in a Computer Network

A school initially bought a computer (with id 1). Over time, the school purchased N-1 additional computers. Each new computer was connected to one of the previously established computers, forming a tree structure. The network can be represented as an undirected tree with N nodes where node 1 is the root.

For each computer i, let \( S_i \) denote the maximum distance (i.e. the number of cables on the unique path) from computer i to any other computer in the network. The distance between two computers is determined by the minimum number of edges between them. For example, consider the tree illustrated below:

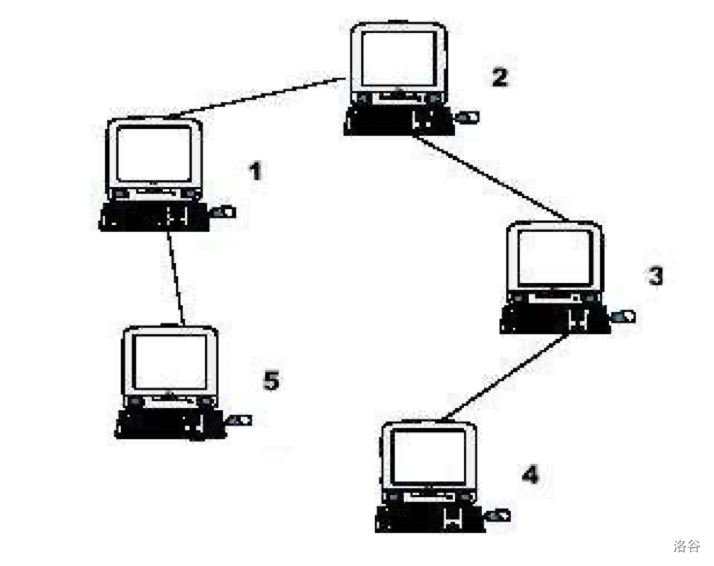
In this example, the distances are as follows:

• From computer 1, the most distant computer is 4 at a distance of 3, so \( S_1 = 3 \).
• From computer 2, the farthest computers are 4 and 5 at a distance of 2, so \( S_2 = 2 \).
• From computer 3, the farthest computer is 5 at a distance of 3, so \( S_3 = 3 \).
• Computers 4 and 5 each have a maximum distance of 4, hence \( S_4 = 4 \) and \( S_5 = 4 \).

Your task is to compute \( S_i \) for every computer \( i \) in the network.

inputFormat

The first line of input contains a single integer \( N \) (1 \( \leq N \leq 10^5 \)), the number of computers. The next \( N-1 \) lines each contain one integer. The \( i\text{-th} \) of these lines (for \( 2 \leq i \leq N \)) contains the integer \( p_i \) (1 \( \leq p_i .

outputFormat

Output \( N \) space-separated integers \( S_1, S_2, \dots, S_N \) where each \( S_i \) is the maximum distance from computer \( i \) to any other computer in the network.

sample

5
1
2
1
3

3 2 3 4 4