Determine if a Graph is a $k$-Trity Graph

We call an undirected graph a $k$-trity graph (for a non-negative integer $k$) recursively as follows:

• For $k=0$, a $0$-trity graph is a graph with exactly one vertex and no edges.
• For $k>0$, a $k$-trity graph is obtained by taking three $(k-1)$-trity graphs, selecting one vertex from each, and adding edges between every pair of the three chosen vertices (thus forming a triangle). The final graph is the union of the three disjoint $(k-1)$-trity graphs and the extra three edges that connect the chosen vertices.

For example, the figure below shows a $3$-trity graph:

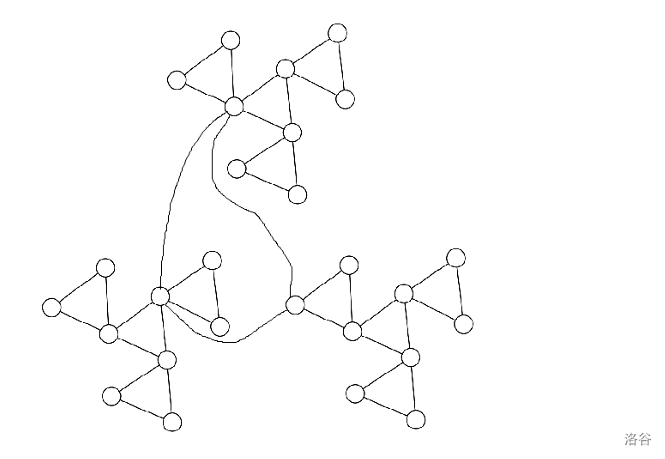
Your task is: Given an undirected graph \(G\), determine whether it is a $k$-trity graph for some non-negative integer $k$.

inputFormat

The first line contains two integers \(n\) and \(m\), denoting the number of vertices and edges of the graph \(G\) respectively. The vertices are numbered from 1 to \(n\).

Each of the following \(m\) lines contains two integers \(u\) and \(v\) (\(1 \le u,v \le n\), \(u \neq v\)), representing an undirected edge between vertices \(u\) and \(v\). There are no duplicate edges.

outputFormat

Output a single line: YES if the given graph \(G\) is a $k$-trity graph for some non-negative integer $k$, or NO otherwise.

sample

1 0

YES