Maximum Parking Spots

You are given a square field consisting of n × n cells. There is an impenetrable wall surrounding the field. You want to design a parking lot on this field. The bottom‐left cell (the exit) must not be used as a parking spot, but every other cell can potentially be assigned as a parking spot.

Each cell of the field is a 1 × 1 square, and the sides of each cell are parallel to the walls. You plan to mark some cells as empty (which will form the passageways/roads that are all connected and include the exit) and assign the remaining cells as parking spots. However, there is an important restriction: every parking spot must have at least one four‐adjacent (up, down, left, or right) empty cell. More precisely, for every parking spot there must exist a cell that is empty and that can be reached from the exit by moving repeatedly in one of the four cardinal directions without passing through any parking spot.

Your task is to maximize the number of parking spots (red cells in the figure below) by choosing a connected set of empty cells (blue, with the exit among them) of minimum possible size such that every parking spot (the remaining white cells) is adjacent to at least one empty cell. One optimal configuration for n = 4 is illustrated below:

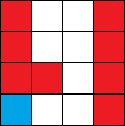
Note: If n = 1 then the only cell is the exit, so no parking spot can be arranged.

Input requirement: A single integer n representing the size of the grid. In this problem, you are to answer the case n = 2023.

Output: Print the maximum number of parking spots that can be arranged under the above conditions.

Mathematical Explanation: Let the total number of cells be \[ n^2 \] . We want to choose a connected set \(R\) (the empty cells including the exit) with minimum size under the condition that every cell not in \(R\) (i.e. every parking spot) has at least one four‐neighbor in \(R\). It can be shown that for n ≥ 2, one can achieve a configuration where the size of \(R\) is \[ \left\lfloor \frac{n^2}{2} \right\rfloor \] (if \(n^2\) is even) or \[ \frac{n^2-1}{2}\] (if \(n^2\) is odd). Consequently, the maximum number of parking spots is \[ n^2 - \left\lfloor \frac{n^2}{2} \right\rfloor = \begin{cases} \frac{n^2}{2}, & \text{if } n^2 \text{ is even},\\[1mm] \frac{n^2+1}{2}, & \text{if } n^2 \text{ is odd.} \end{cases} \] In particular, when n = 2023 (and \(2023^2\) is odd) the answer is \[ \frac{2023^2+1}{2} = \frac{4\,092\,529+1}{2} = 2\,046\,265. \]

inputFormat

The input consists of a single line containing one integer n (1 ≤ n ≤ 10^5). For this problem, you should output the answer for n = 2023.

outputFormat

Output one integer – the maximum number of parking spots that can be arranged on an n × n grid under the given conditions.

sample

1

0